https://www.acmicpc.net/problem/2133
2133번: 타일 채우기
문제 3×N 크기의 벽을 2×1, 1×2 크기의 타일로 채우는 경우의 수를 구해보자. 입력 첫째 줄에 N(1 ≤ N ≤ 30)이 주어진다. 출력 첫째 줄에 경우의 수를 출력한다. 예제 입력 1 복사 2 예제 출력 1 복사 3 힌트 아래 그림은 3×12 벽을 타일로 채운 예시이다....
www.acmicpc.net
먼저 문제를 설명하기 전에 좀 도움(?)이 되는 설명을 하자면..
[1,2,3,4]로 만들수 있는 경우의 수 중에, 만약 천의 자리가 1로 고정되어 있다면 만들 수 있는 순열의 종류는 (n-1)!이다. 한 자리가 고정되어 있기 때문에 나머지 3개의 숫자로 만들 수 있는 순열의 개수를 세어주면 된다.
이 문제도 같은 논리로 동작한다.
일단 n이 홀수인 경우는 타일을 채울 수 없기 때문에 n이 짝수인 경우만 보자.
n=2인 경우 : dp[2] = 3

n=4인 경우 : dp[4] = dp[2] * 3 + dp[0] * 2
길이가 4인 경우는 가장 오른쪽에 3x2이 고정되어 있다 생각하고 n=2인 경우를 구한다. 근데 가장 오른쪽에 고정되어 있는 도형의 개수가 3개이기 때문에 3을 곱해준다.

하지만 4인 경우는 n=2인 경우와 아래와 같이 2개의 모양이 더 숨어있다. 이는 n >=4인 경우에만 해당한다(물론 홀수는 제외). 4이전에는 3x2도형만 신경쓰면 되는데, 4부터는 도형이 2개 추가되었다.

그렇다면 우리는 이렇게 생각할 수 있다. 가장 오른쪽에 3x2도형이 고정된 경우와 추가된 도형이 오른쪽에 고정된 경우 총 2번을 구해야 겠네 ? 당연 구해야 한다. 새로추가된 도형의 가로길이가 4이고, 도형의 종류가 2개이기 때문에 dp[i-4] * 2를 더해준다.
(사실 n=4 인 경우, 새로 추가된 도형은 가로가 4이기 때문에 왼쪽에 다른 도형을 붙일 수가 없다. 하지만 새로운 도형이 생겼기 때문에 2를 더해주어여 한다.)

n=6인 경우 : dp[6] = dp[2] * 3 + dp[2] * 2 + dp[0] * 2
n이 4이상 부터는 3x2도형 말고 다른 도형이 추가되었기 때문에 그 도형의 경우의 수까지 더해주어여 한다. 근데..n=6인 경우는 n=4인 도형과 모양이 다르다...

그렇기 때문에 n=6인 경우는 n=6와 n=4인 경우를 각각 dp[i]에 더해주어야 한다.
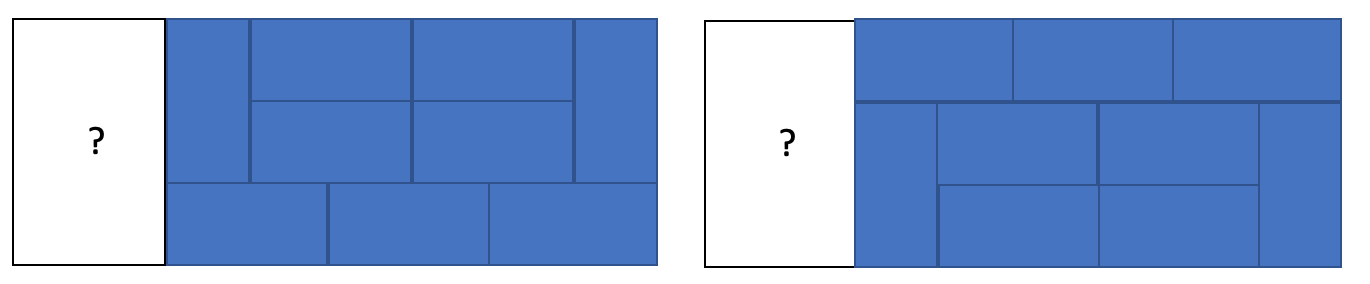
n=8인 경우 : dp[6] = dp[2] * 3 + dp[4] * 2 + dp[2] * 2 + dp[0] * 2
....마찬가지로 새로 추가된 도형을 dp[i]에 계속 더해주어여 하는데 이때 n이 4,6,8인 경우를 모두 dp[i]에 더해주어여 한다.
n=10인 경우.......
#include <iostream>
using namespace std;
int main()
{
int n;
cin >> n;
int dp[31] = {0};
dp[0] = 1;
dp[2] = 3;
for (int i = 4; i <= n; i++)
{
dp[i] = dp[i - 2] * 3; // 2x3 도형을 가장 오른쪽에 두는 경우, 2x3 도형이 3개이기 때문에 *3을 해준다
for (int j = 4; j <= i; j += 2)
{
dp[i] += dp[i - j] * 2; // n=4부터는 새로운 도형이 추가된다. 하지만 n이 4,6,8,10...일때 도형의 모양이 모두 다르기 때문에 각각 dp[i]에 더해준다.
}
}
cout << dp[n];
return 0;
}'알고리즘 문제' 카테고리의 다른 글
| [알고리즘 문제] 백준2225 - 합분해 (0) | 2020.04.10 |
|---|---|
| [알고리즘 문제] 백준9461 - 파도반 수열 (0) | 2020.04.10 |
| [알고리즘 문제] 백준1699 - 제곱수의 합 (0) | 2020.04.09 |
| [알고리즘 문제] 백준2579 - 계단 오르기 (0) | 2020.04.08 |
| [알고리즘 문제] 백준1912 - 연속합 (0) | 2020.04.05 |
