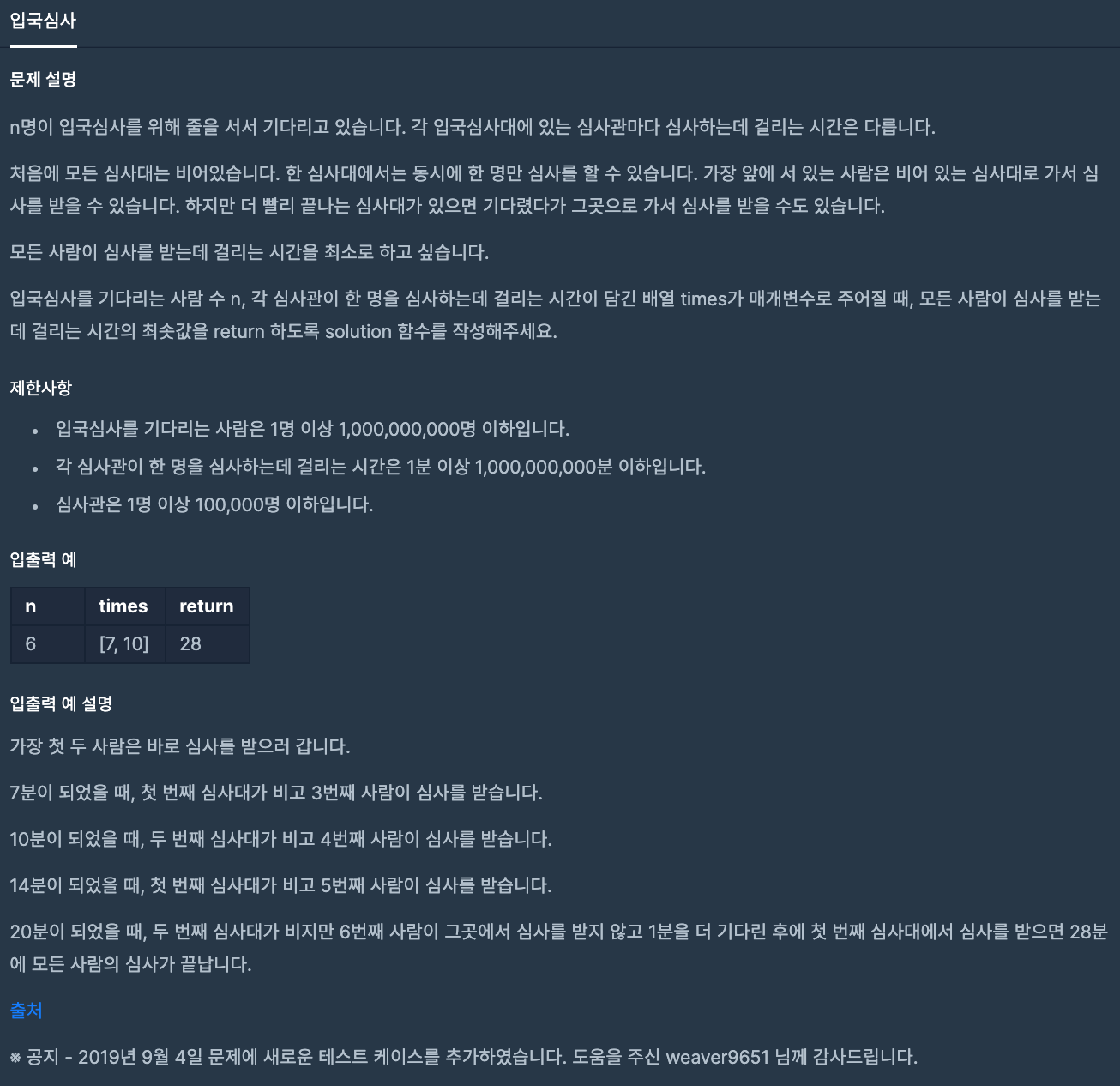
문제 분류는 이진탐색 문제이다.
쉽게 설명하면, 술게임 중에 소주병 뚜껑에 적힌 숫자를 맞추는 게임이 있다. 우리는 그 숫자에 대한 범위(0~100)만 안 상태에서 반씩 줄여가면서 숫자를 찾는다. 50을 말했을 때 up이면 다시 50~100에서 숫자를 찾고 75를 외쳤을 때 down인 경우 50~75....이런 식으로 숫자를 찾아가는 과정이다.
이와 비슷한 논리로 문제를 풀어 나갈 수 있다.
생각해보면 문제는 "모든 사람이 심사를 받는데 걸리는 최소 시간"을 구하는 문제이다. 이말은 즉, "모든 사람이 심사를 받을 수 있는 시간"의 값이 여러개 존재하고 그 중에서 최소 시간을 구하라는 것이다. 여기서 우리는 "모든 사람이 심사를 받을 수 있는 여러개의 값" 중에서 최소 시간의 값을 구하는 방법으로 이진탐색을 사용한다.
우리는 특별하게 fail과 success라는 변수를 사용한다. 코드에서 이 변수들이 의미하는 값을 이해하는게 엄청 중요한데,
success : 무조건 모든 사람이 심사를 받을 수 있는 시간 / fail : 무조건 모든 사람이 심사를 받을 수 없는 시간
으로 정의할 수 있다.
예를 들어, 첫번째 라인의 심사관은 28분 동안 4명의 사람을 심사할 수 있고(28 / times[0]), 두번째 라인의 심사관은 28분동안 2명의 사람을 심사할 수 있다(28 / times[1]), 그럼 입국심사대에서 28분동안 총 6명의 사람을 심사할 수 있게 된다.
반면에 시간이 10분이라고 하면 각각의 라인의 심사관은 1,1 씩 검사하게 되므로 10분동안 총 2명의 사람을 심사할 수 있다.
결과적으로 문제에서 총 6명의 사람을 심사해야 하기 때문에 success에는 28, fail에는 10이라는 값이 들어가게 된다. 28에는 무조건 모든 사람을 심사할 수 있고, 10일 때는 무조건 모든 사람을 심사할 수 없기 때문이다. 우리가 그렇게 정의를 했다.
하지만 여기서 우리는 28이라는 값이 "최소"의 값이라고 확신할 수 있을까?(문제의 답이지만 우리는 모른다고 가정한다) 그렇지 않다, 왜냐하면 10~28 사이에 "최소"를 만족하는 새로운 값이 존재할 수도 있기 때문이다. 다시 가운데 값인 19에서 "모든 사람을 심사할 수 있는"지 검사를 한다. 만약 검사를 할 수 있다 ? 그럼 success에 넣고 그렇지 않으면 fail에 넣는다.
위의 과정을 success와 fail값 차이가 1이 날때까지 반복한다. 이런 과정을 통해 결국에는 success에 "최소"의 값이 들어가게 된다.
이렇게 길게 설명한 이유는, 다른 사람들의 설명을 보면 success, fail를 설정해놓고 정작 그 변수들이 의미하는 것을 설명해놓지 않았기 때문이다. 실제로 코드로 구현해보면 정말 간단하다. 하지만 이런 "방법"을 생각해 내는게 어렵다.
코드에서 fail과 success에 초기화 한 값의 의미를 살펴보면,
fail은 "무조건 모든 사람이 심사를 받을 수 없는 시간"이다. 그렇기 때문에 1인 시간에는 어떤 손님도 심사할 수 없기 때문에 1로 초기화 하였다. 근데 굳이 1이 아니여도 상관없다. 0을 하던 음수값을 하던 어쨋든 그 값에서는 fail변수의 정의를 만족한다.
success는 "무조건 모든 사람이 심사를 받을 수 있는 시간 "인데, 그 값중에 가장 큰 값은 언제일까 ? 아마 모든 사람을 심사할 수 있는데 시간이 정말 오래 걸리는 최악의 경우, 즉 심사하는데 시간이 가장 오래 걸리는 심사관이 모든 사람들을 심사하는 경우일 것이다.
#include <string>
#include <vector>
#include <algorithm>
#include <iostream>
using namespace std;
long long solution(int n, vector<int> times) {
long long fail = 1; // 무조건 처리할 수 없음.
long long success = (long long)times.back() * n; // 무조건 처리할 수 있음.
while(fail+1 < success){
long long mid = (fail+success)/2;
long long peoples = 0;
for(int i=0;i<times.size();i++){
peoples +=(mid/times[i]); // mid시간 동안 처리할 수 있는 사람들의 수.
}
if(peoples < n){ // 처리할 수 없다.
fail = mid;
}else{ // 처리할 수 있다.
success = mid;
}
}
return success;
}
'알고리즘 문제' 카테고리의 다른 글
| [알고리즘문제] 프로그래머스 - 보행자 천국 (0) | 2020.02.04 |
|---|---|
| [알고리즘문제] 프로그래머스 - 베스트 앨범 (0) | 2020.02.03 |
| [알고리즘문제] 프로그래머스 - 정수 삼각형 (0) | 2020.01.16 |
| [알고리즘문제] 프로그래머스 - 피보나치 수 (0) | 2020.01.06 |
| [알고리즘문제] 프로그래머스 - 최대값과 최솟값 (0) | 2020.01.06 |



