이번시간에는 힙에 대해서 공부해보겠습니다.
힙은 최댓값과 최솟값을 찾아내는 연산을 빠르게 하기 위해 고안된 완전이진트리(마지막 레벨-1은 모두 채워져 있고, 마지막 레벨은 노드가 왼쪽부터 구조를 기본으로 한 자료구조) 입니다.
영단어 힙(heap)은 '무엇인가를 차곡차곡 쌓아 올린 더미'라는 뜻을 지니고 있습니다. 힙에서 부모의 값은 항상 자식(들)의 값보다 크거나(Max Heap, 최대힙), 작아야(Min Heap, 최소힙)하는 규칙이 있습니다. 따라서 루트 노드에는 항상 데이터들 중 가장 큰 값, 혹은 가장 작은 값이 저장되어 있기 때문에 최대값,최솟값을 O(1)만에 찾을 수 있습니다.
단순히 최대값,최솟값을 O(1)안에 찾기 위해서라면 "항상 완전 이진 트리의 형태여야 한다"는 조건을 만족시킬 필요는 없습니다. 완전 이진 트리를 사용하는 이유는 삽입/삭제O(logN)의 속도 때문입니다.
구조

일반적으로 힙을 배열로 구현합니다. 편의상 0번째 index는 사용하지 않습니다. 이런식으로 배열으로 구현했을 때, 각 노드간의 규칙을 발견할 수 있으며, 이 규칙을 사용하여 삽입/삭제를 구현할 수 있습니다.
parent index = i/2
left child = 2*i
right child = 2*i+1

최대힙(Max Heap) : 부모 노드의 값이 자식 노드의 값보다 항상 큰 구조
최대힙(Min Heap) : 부모 노드의 값이 자식 노드의 값보다 항상 작은 구조
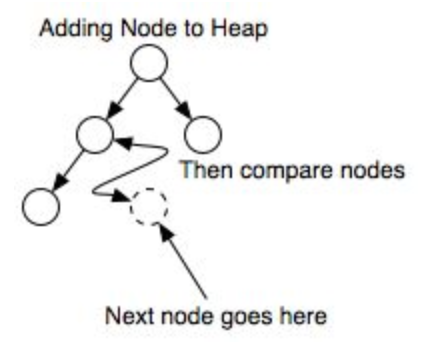
삽입연산
-
가장 끝의 자리에 노드를 삽입합니다
-
그 노드와 부모 노드를 서로 비교합니다.
-
규칙에 맞으면 그대로 두고, 그렇지 않으면 부모와 교환합니다.
-
규칙에 맞을 때까지 3번 과정을 반복합니다.
public void insertHeap(int item) {
int i = ++heapSize;
while ((i != 1) && (item > itemHeap[i / 2])) {
itemHeap[i] = itemHeap[i / 2];
i /= 2;
}
itemHeap[i] = item;
}
삭제연산

-
루트 노드를 제거합니다.
-
루트 자리에 가장 마지막 노드를 삽입합니다.
-
올라간 노드와 그의 자식 노드(들)와 비교합니다.
-
조건에 만족하면 그대로 두고, 그렇지 않으면 자식과 교환합니다.
-
최대 힙
-
부모보다 더 큰 자식이 없으면 교환하지 않고 끝냅니다.
-
부모보다 더 큰 자식이 하나만 있으면 그 자식하고 교환하면 됩니다.
-
부모보다 더 큰 자식이 둘 있으면 자식들 중 큰 값과 교환합니다.
-
-
최소 힙
-
부모보다 더 작은 자식이 없으면 교환하지 않고 끝냅니다.
-
부모보다 더 작은 자식이 하나만 있으면 그 자식하고 교환하면 됩니다.
-
부모보다 더 작은 자식이 둘 있으면 자식들 중 작은 값과 교환합니다.
-
5. 조건을 만족할 때까지 4의 과정을 반복한다.
public int deleteHeap() {
int parent, child;
int item, temp;
item = itemHeap[1];
temp = itemHeap[heapSize--];
parent = 1;
child = 2;
while (child <= heapSize) {
if ((child < heapSize) && (itemHeap[child] < itemHeap[child + 1])) {
child++;
}
if (temp >= itemHeap[child]) {
break;
}
itemHeap[parent] = itemHeap[child];
parent = child;
child *= 2;
}
itemHeap[parent] = temp;
return item;
}
힙 정렬
#include <iostream>
#include <vector>
using namespace std;
int number = 10;
int heap[10] = {6,2,10,8,9,3,11,15,21,40};
// max heap
void heapify(int i){
int c = 2 * i + 1; // 왼쪽 노드, index가 0부터 시작해서 +!
if(c < number && heap[c] < heap[c+1]){ // 오른쪽 노드가 있고, 오른쪽이 더 크면
c++;
}
if(heap[i] < heap[c]){
int temp = heap[i];
heap[i] = heap[c];
heap[c] = temp;
}
if(c <= number/2){ // 아래 부분에서 heap이 아닐 수 있으니 재귀적으로 다시 확인
heapify(c);
}
}
int main(){
for(int i=number-1/2; i>=0;i--){ // 4 3 2 1 0
heapify(i);
}
for(int j=0;j<number;j++){
cout << heap[j] << ' ';
}cout << "\n\n";
for(int i=number-1;i>=0;i--){
for(int j=0;j<number;j++){
cout << heap[j] << ' ';
}cout << "\n";
int temp = heap[0];
heap[0] = heap[i];
heap[i]=temp;
int root = 0;
int c = 1;
do{
c = (2 * root) + 1;
if(c < i-1 && heap[c] < heap[c+1]){ // 자식중에 더 큰값
c++;
}
if(c < i && heap[root] < heap[c]){ // 루트보다 자식이 크다면 교환
temp = heap[root];
heap[root] = heap[c];
heap[c] = temp;
}
root = c;
}while(c < i);
}
for(int i=0;i<number;i++){
cout << heap[i] << " ";
}
return 0;
}'computer science > 자료구조' 카테고리의 다른 글
| [자료구조] 그래프(Graph) (0) | 2019.07.17 |
|---|---|
| [자료구조] 트리(Tree) (0) | 2019.07.02 |
| [자료구조] 큐(Queue) (0) | 2019.06.20 |
| [자료구조] 배열과 list(LinkedList, ArrayList) (0) | 2019.06.02 |
| [자료구조] 스택(Stack) (0) | 2019.06.01 |



